关于H-功能
H函数(加速信号包络处理)
(1)H函数的理论
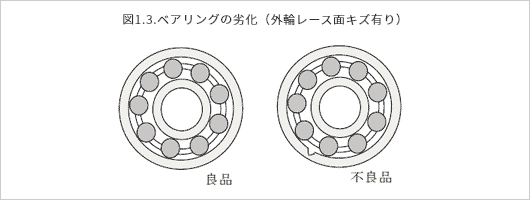
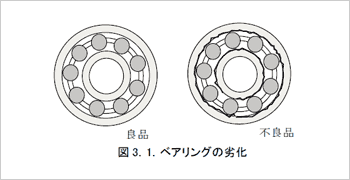
让我们把机械元件的劣化看作是一个轴承。当轴承的外圈被划伤时,就会出现转弯的假设(图1.3)。
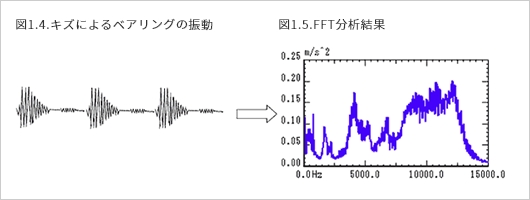
当轴承旋转时,划痕被轴承的滚珠(滚动体)击中,并产生了冲击。这种冲击导致外圈转动振动,并传递给轴承座。外圈的表面转动振动。(图1.4)。
FFT分析仪对这一振动进行分析和轴承的指示频率特性。冲击主要激发了轴承的共振点。(图1.5)。
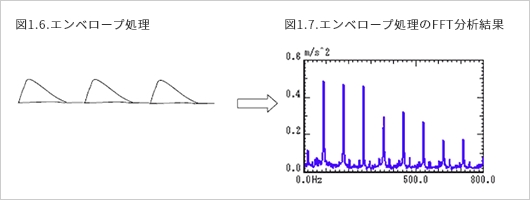
无论旋转速度如何,除了振动变得比正常分布的轴承大之外,这种特性几乎没有什么特点。然而,如果由划痕引起的轴承振动被整顿的绝对值,然后通过低通滤波器(图1.6.)。 这个过程被称为包络处理。这个包络检测波形被FFT分析仪清晰地检测出来,用于频率分析和周期打划痕。(图1.7.)
这个过程在IMV中被称为H函数
仅仅考虑有效值、有效值和峰值,情况并非如此,但实际的波形表明,在正态分布的轴承中也会出现尖锐的加速度波形。H函数对这种波形的分析具有噪声的作用。通过H函数处理,峰值被稳定下来。
(2)H函数的理论
H函数是对2kHz~15kHz的高频振动加速度进行包络检测的信号处理。由于是高频振动,所以它能很好地穿过金属内部。高频振动几乎不受Fix部件的影响,除非将振动转为隔离,否则就会传播。(相反,振动水平的变化受测量部件结构和测量位置的位移影响。)
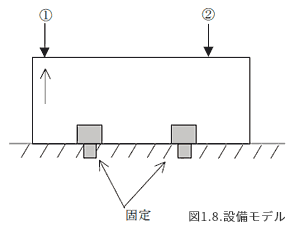
- 考虑一个有测量部件①和②的设备
- 由于V函数(速度)的位移振幅很大,振动被衰减,几乎不在固定部分传播。
- 由于位移振幅非常小,H函数几乎不受固定部分的影响。
H函数在②中也能被检测到
当机械部分发生错误时,可检测到高频振动。轴承老化、润滑脂不足或细微的动态平衡错误都可被检测到。
(然而,仅凭H函数的振动水平的变化不能区分异常的金德)
它对旋转速度的变化反应灵敏。可以检测到轴承老化、油脂不足或细微的动态平衡错误。(然而,仅凭H功能的振动水平的变化不能区分异常的种类)
H-函数作为V-函数(速度)的一个辅助函数 尽管V型函数基本上是捕捉设备劣化的最佳方式,但当轴承等部件被刮伤时的高频振动很难用V型函数来检测。
加速度可以检测到轴承的劣化,但可以获得更稳定的信号处理(包络)的可靠性。
(3)H函数的信号处理
脉冲
脉冲是在部件恶化时产生的
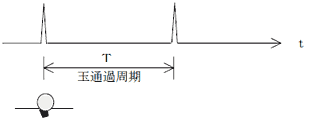
共振系统(设施)
加速器
当脉冲通过共振系统(设施)时,它被脉冲所激发。对于内径10mm以上的滚动轴承,f0低于15kHz
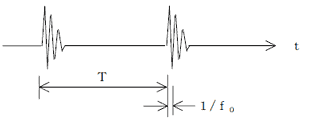
电荷放大器
带通滤波器
2kHz到15kHz
只提取有零件劣化的高频振动。
消除由劣化以外的其他因素引起的低频成分和难以测量的高频成分。
绝对值整流
绝对值对高频波形进行整流
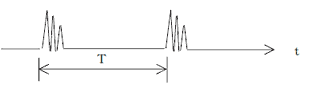
低通滤波器
削减超过1kHz的成分
删除1kHz以上的成分
转换波形为类似脉冲的波形
消除除恶化引起的振动以外的脉冲噪音
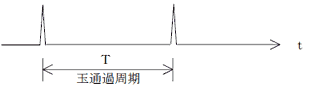
包络过程是指在共振系统中激发的高频分量被绝对值整流,高频分量被低通滤波器去除,原来的低频分量(球通恶化部分的频率分量)被转为提取的过程。
H函数C.F
(1)峰值(PEAK)与有效值(RMS)之比,有效值(RMS)称为C.F.(波峰因子)
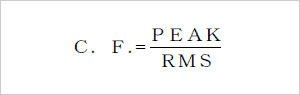
- 当轴承是正常分布时,有效值、有效值和峰-峰值都很小
- 当轴承被划伤时,峰值增加。伤痕越大,峰间值越大。然而,RMS值、有效值却没有那么大。
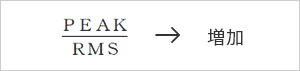
-
随着划痕的增加,轴承的整个滚道表面逐渐变得粗糙。在这种情况下,峰-峰上升速度下降,但有效值、均方根值逐渐增加。
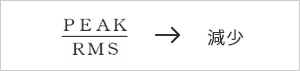
- 峰值因子的概念
| 道路 | 说明 |
|---|---|
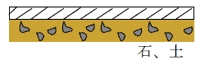
|
石质、土质铺设的道路 几乎没有振动传到汽车上。 轴承。正面 |
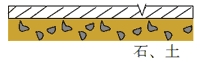
|
可以移除部分铺装路面。 当汽车撞上铺装区时,瞬间转为振动 轴承。划痕 |
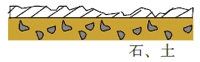
|
人行道表面摇摇欲坠 当汽车运行时,会有振动。 轴承: 粗糙 粗糙的表面,变质 |
(2)C.F.(CREST FACTOR)表示波形状态,所以受振动传输段路径的影响不大
当速度为10Hz~1000Hz转为测量时,振动产生部分和振动测量点之间的空间可以被视为一个刚性体。换句话说,在测量点上,振动发生器的振动水平可以以相当高的精度被捕获,高精度。
但是,当高频(2kHz~100kHz)的加速度像轴承一样被划伤后转而测量时,在振动产生部分和振动测量点之间不能被视为刚体。测量点的振动水平与振动发生器的振动水平不一致。 即使在这些情况下,如果C.F.转为测量,其值表示为峰值和有效值之间的比率,有效值(PEAK/RMS和波形的粗略状态),因此,无论振动水平值如何,都可以用于恶化判断。
| 波形 | PEAK | RMS |
|---|---|---|
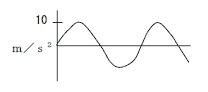 |
10m/s2 | 7m/s2 |
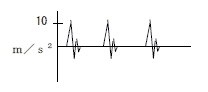 |
10m/s2 | 7m/s2 |
例如 / 峰值相同但均方根值不同的例子,有效值
(3)C.F.的使用
请务必将C.F.与RMS值、有效值一起使用,以便对其进行趋势分析。
当均方根值、有效值超过正常分布值并进入警戒区时,必须检查C.F.值的趋势分析图。
当均方根值、有效值表示正常分布时,C.F.的变化意义不大。