H関数に関して
H関数(加速度信号のエンベロープ処理)
(1)H関数の理論
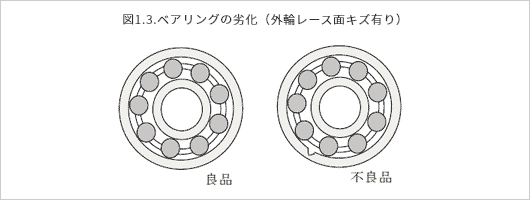
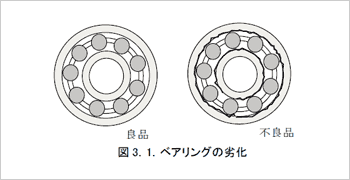
機械要素の劣化をベアリングに例えて考えてみましょう。ベアリングの外輪にキズがついたと仮定します。(図1.3.)
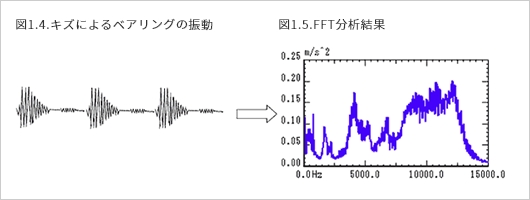
ベアリングが回転すると、キズにベアリングの玉(転動体)があたるので衝撃波が発生します。この衝撃波により外輪が振動し、軸受けハウジングに伝わり、その表面が振動します。(図1.4.)
この振動をFFTアナライザで分析するとベアリングの周波数特性が表示されます。 衝撃波によってベアリングの共振点が主に 励振されます。(図1.5.)
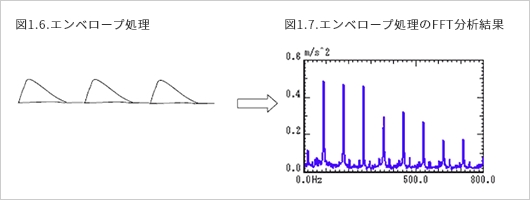
この特性は、回転数に関係なく、正常ベアリングより振動が大きくなる以外のキズによる特徴はあまり出てきません。しかし、キズによるベアリングの振動を絶対値整流し、ローパスフィルタに通すと(図1.6.)になります。この様な処理をエンベロープ処理といいます。 このエンベロープ検波波形をFFTアナライザで周波数分析するとキズに玉が当たる周期がはっきり検出されます。(図1.7.)
この様な処理をIMVではH関数と呼んでいます。
実効値とピーク値のみを考えるなら、わざわざこの様な処理をする必要が無いように、しかし実際の波形を見るとスパイク状の加速度波形が正常ベアリングにも発生します。そのような波形分析する上でのノイズをとる働きがH関数にはあります。H関数処理することでピーク値が安定します。
(2)H関数の特徴
① 2kHz~15kHzの高周波振動加速度をエンベロープ検波による信号処理したものが、H関数です。高周波振動なので金属内部をよく伝わります。高周波振動は固定部の影響をほとんど受けず、振動を絶縁しない限り、伝わっていきます。(むしろ、振動レベルの変化には測定部位の構造、測定場所のズレの影響を受けます。)
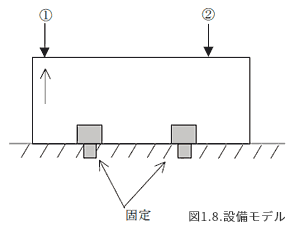
- 測定部位①、②をもつ設備について考えてみます。
- ①で異常による振動発生。 V関数(速度)の変位振幅が大きいため固定部分でその振動は減衰して伝わりにくい。②で速度は減衰して小さくなります。
- H関数の変位振幅が非常に小さいため、固定部分の影響をほとんど受けない。
②でもH関数を検出できます。
② 機械部品に異常が発生した時の高周波振動を検出します。 軸受劣化、グリス切れ、微妙な動バランス異常が検出できます。
(しかし、H関数の振動レベルの変化だけでは、異常の種類の区別まではできません。)
③ 回転数の変化に敏感に反応します。軸受劣化、グリス切れ、微妙な動バランス異常が検出できます。(しかし、H関数の振動レベルの変化だけでは、異常の種類の区別まではできません。)
④ V関数(速度)の補助関数としてのH関数
設備の劣化をとらえるには、基本的にV関数を使用すると良いのですが、ベアリングのような部品にキズがついた場合の高周波振動は、V関数では検出が困難です。
加速度でベアリングの劣化を検出できますが、より安定な信号処理(エンベロープ処理)して、信頼性のあるデータを得ることができます。
(3)H関数の信号処理
インパルス
部位の劣化でインパルスが発生します。
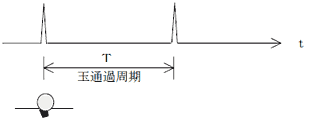
共振系(設備)
加速度ピックアップ
共振系(設備)をインパルスが通過するとインパルスにより励振します。f0は内径10mm以上のころがり軸受けでは15kHz以下にあります。
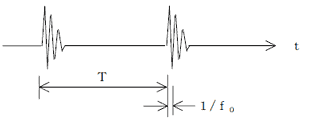
チャージアンプ
バンドパスフィルタ
2kHz~15kHz
部品劣化による高周波振動のみ抽出します。
劣化以外の他の要因で発生する低周波成分及び測定の困難な高周波成分を取り除きます。
絶対値整流
高周波波形を絶対値整流します。
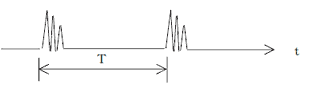
ローパスフィルタ
1kHz以上をカット
1kHz以上の成分を取り除きます。
波形をインパルスに似た波形に変換します。
劣化による振動以外のパルス状のノイズを取り除きます。
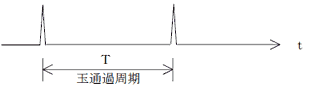
共振系で励振された高周波成分を絶対値整流し、ローパスフィルタで高周波成分を除去し、本来の低周波成分(劣化部分を玉が通過する周波数成分)を抽出する方法をエンベロープ処理と呼びます。
C.F.
(1)ピーク値(PEAK)と実効値(RMS)の比をC.F.(クレストファクタ)と呼びます。
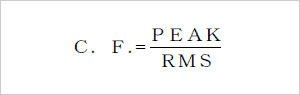
- ベアリングが正常な時、実効値、ピーク値とも小さな値です。
- ベアリングにキズが入るとピーク値が大きくなります。キズが大きくなるにつれ、
ピーク値が大きくなりますが、実効値は、それほど大きくなりません。
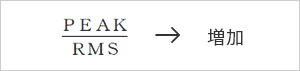
-
キズが大きくなると、ベアリングのレース面全体が次第に荒れてきます。この状態になるとピーク値の増大スピードは小さくなりますが、実効値は次第に大きくなります。
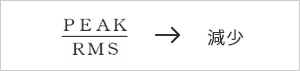
- クレストファクタの考え方
| 道路 | 説明 |
|---|---|
|
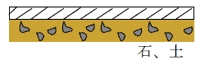
舗装したばかりの道路 ほとんど車に振動が伝わってこない。 ベアリング:正 |
|
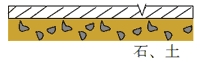
部分的に舗装がとれる。 舗装のとれた所に車があたると瞬間的に振動する。 ベアリング:キズ |
|
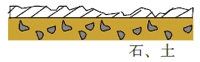
舗装面が崩れている。 車が走るとガタガタ振動する。 ベアリング:面荒れ、劣化 |
(2)C.F. (CREST FACTOR) は波形の状態を表すので、振動伝達部の経路の影響をあまり受けません。
10Hz~1000Hzの速度を測定する時、振動発生部と振動測定点との間は、剛体とみなすことができます。 つまり、測定点で振動発生部の振動レベルをかなり高精度でとらえることができることになります。
しかし、ベアリングのようにキズがついた時の高周波(2kHz~100kHz)の加速度を測定する時は、振動発生部と振動測定点との間は剛体とみなすことができません。測定点の振動レベルは、振動発生部の振動レベルとは一致してないことになります。 こういった場合でもC.F.を測定してあれば、その値はピーク値と実効値の比率(PEAK/RMS、波形の大まかな状態)で表されますので振動レベルの値そのものには関係なく、劣化の判断材料に利用することができます。
| 波形 | PEAK | RMS |
|---|---|---|
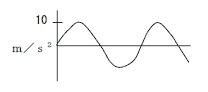 |
10m/s2 | 7m/s2 |
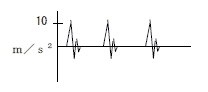 |
10m/s2 | 1m/s2 |
ピーク値は同じでも実効値が異なる例
(3)C.F.の使用方法
C.F.値は、必ず実効値と併用して傾向管理して下さい。
実効値が正常値を超え、要注意領域に入った場合に、C.F.値の傾向管理グラフをチェックする必要があります。
実効値が正常値を示している場合のC.F.値の変化はあまり意味がありません。