The technique called “Clipping” is applied by almost every vibration controller in the world for almost every Random vibration test performed.

Why do “Clipping”?

When a drive signal of a random vibration controller is analysed in the aspect of its amplitude distribution, it will be found, that its probability density function (PDF) equals the shape of the “Normal Distribution”.

 

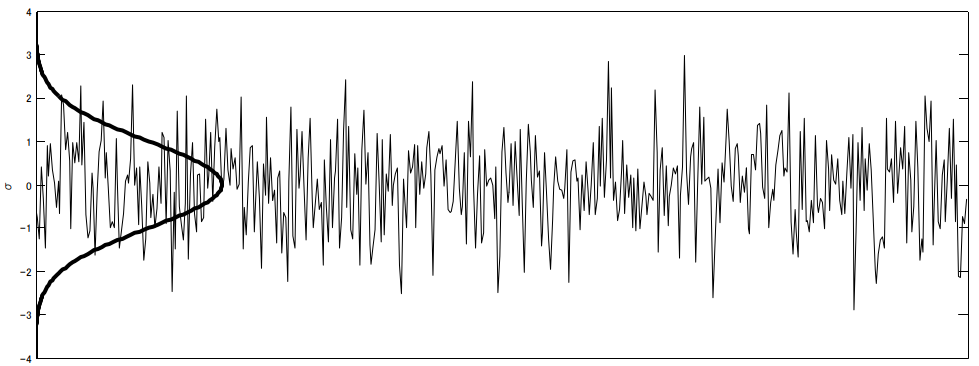
Figure 1: Normal Distribution and Random Vibration Drive signal

The normal distribution represents the distribution of data, as it often occurs in nature. The normal distribution is “built up” symmetrically around the average value or expected value. For example, most people (of the same gender) have an average height, but only very few are very large or very small.

According to the natural distribution: (very) high level voltage peaks will naturally occur as part of the drive signal of a random vibration controller.

• When the excitation level for a Random vibration test is low compared to the rating of the shaker system, this would not cause any problems
• When the test is done at a level around the system rating, a high-level drive signal peak could cause an abort status of the system.

To avoid such cases to happen, the values exceeding a certain level are eliminated from the drive signal.

This technique is called “Clipping” and there are different solutions, how to do it.

Hard-Clipping

By applying Hard-Clipping to a drive signal, values exceeding a certain limit are removed from the signal.

 

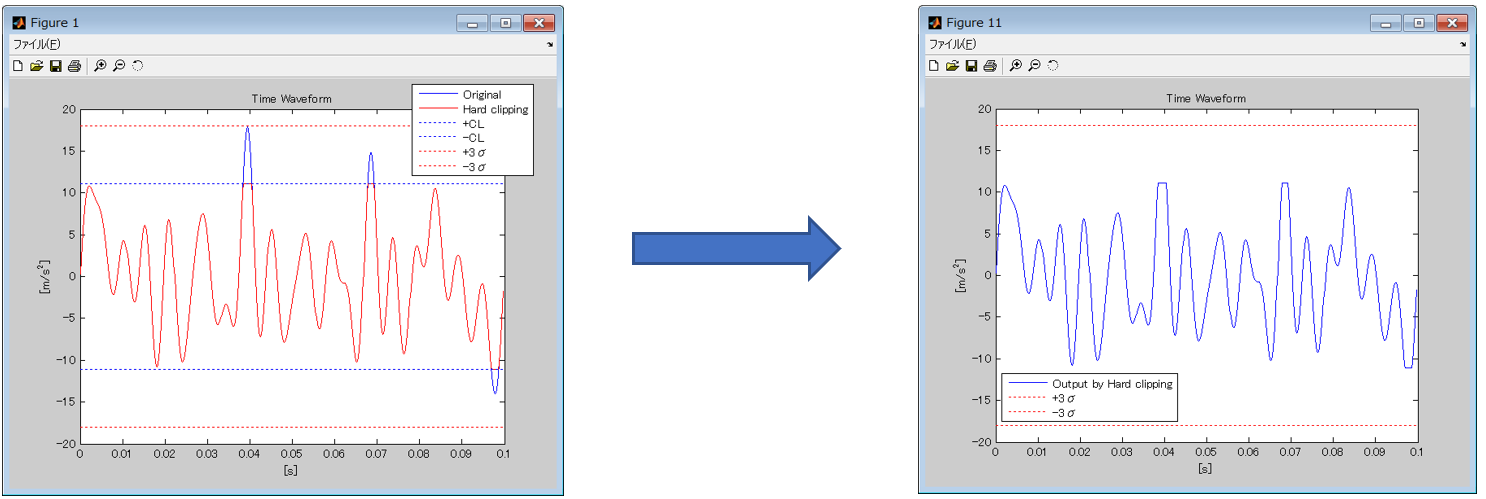
Figure 2: Hard-Clip procedure and resulting drive signal

Cause and Effect in the frequency range

According to the Fourier theorem, a rectangular signal will cause harmonic components over a wide frequency range.

 

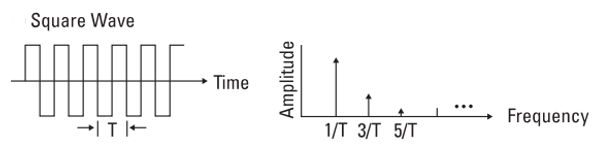
Figure 3: Fourier analysis (frequency domain) of a square wave signal (time domain)

The smaller the rectangular shape of the Hard-Clipped area, the more does it resemble the shape of an impulse. According to the Fourier theorem, an impulse will induce additional frequency components continuously spread over a wide frequency range.

 

Figure 4: Fourier analysis (frequency domain) of a pulse-shaped signal (time domain)

When the drive signal is being hard-clipped, this is imposing a shape in between “Rectangular” and “Impulse” to the output signal.

 

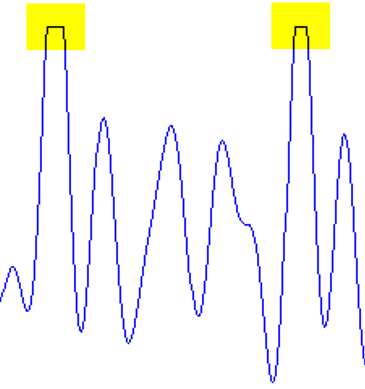
Figure 5: Example of a Hard-Clipped output signal sequence

According to Figure 3 and Figure 4, Hard-Clipping of a signal is creating additional frequency components for any hard clipped signal. As Hard-Clipping would naturally occur continuously, the total of additional frequency components can be understood as Clipping-Induced-Noise (CIN).

In other words, the components of the drive spectrum are “smeared” by CIN and the delicate structure of the original signal is covered.

CIN excites the resonances of a system. If these resonances are in the audible frequency band, the response of the system can become perceptive as a high frequency ringing noise.

Soft-Clipping

The patented IMV-Soft-Clipping method is completely avoiding creating “sharp edges” in the clipped signal by using a sophisticated technique in the frequency domain.

Accordingly, additional undesired generation of noise components is suppressed when keeping the frequency components of the drive signal controlled just as desired. By limiting the peak value of the time waveform within the required level, the PSD of the drive output signal remains unchanged.

By applying the IMV-Soft-Clipping method there are the following potential advantages:

• Noise is reduced, dynamic control range is increased
• Resonances in the test setup are no longer excited unwillingly, leading to better control results and more accurate testing
• Occurrence of unwanted amplifier-tripping is reduced

See below links for audible examples:

• Example for Random-Test: Hard Clipping, ringing noise is audible.
• Example for Random-Test: Soft Clipping, no ringing noise.

cover photo © Roman Safreider / stock.adobe.com