Schulungen zum Einsatz des neuen Prüfverfahrens

• Wahrscheinlichkeitsdichtefunktion
• Der Parameter Kurtosis
• Skewness “Schiefe”, ein Maß für die Symmetrie
• Regelung für nicht-gaußsche Signale
• Vereinzelte und ständige Spitzen

Karosserie, Fahrwerk und Interieur von Fahrzeugen sind dauerhaft dynamischen Belastungen ausgesetzt. In Produkttests und Transportsimulationen werden die Leistungsfähigkeit und Steifigkeit der Komponenten unter realen Bedingungen auf die Probe gestellt. Bislang verlief das Verfahren häufig mit einer rauschförmigen Anregung, bei der für die Amplitudenhäufigkeit die Normalverteilung zu Grunde gelegt wurde. Ab sofort können IMV Schwingerreger auch nach nicht-gaußscher Verteilung prüfen. Möglich macht das eine neue Software, die neben den herkömmlichen Eigenschaften für eine klassische rauschförmige Anregung zwei neue Parameter einbindet: Kurtosis („Spitzigkeit“) und die Skewness („Schiefe“).

Reale Spitzenwerte sind oft höher

„Mit Hilfe des nicht-gaußschen Verfahrens wird versucht“, so Dipl.-Ing. (FH) Martin Engelke, Marketing und Sales Manager IMV, „die zur Anregung im Labor verwendeten Signale möglichst an die tatsächlich auftretenden Bedingungen anzupassen, um eine identische Belastung zu erzielen.“ Die Prüfergebnisse hängen dabei naturgemäß stark von der Art und der Methode des unter Laborbedingungen erzeugten mechanischen Stresses ab. „Messungen bei Fahrzeugtests haben ergeben, dass die real auftretenden Spitzenwerte oft höher sind und die Häufigkeit der Amplituden einer abweichenden Verteilung entsprechen“, so Engelke weiter.

Bessere Realitätsabbildung mit der nicht-gaußschen Verteilung

Früher wurden häufig sinusförmige Signale verwendet. In den vergangenen Jahren gewann immer mehr die rauschförmige Anregung an Bedeutung, da sie der realen Belastung besser entspricht. Grundlage der rauschförmigen Anregung ist die Normalverteilung. Seit kurzem kommt verstärkt die nicht-gaußsche Verteilung zum Einsatz. Für den Ingenieur ist dabei wichtig, die Natur der Signale gut zu verstehen. Er muss Schutzfunktionen für den Prüfling vor zu großen Spitzen und den Schutz des Schwingprüfsystems genauso berücksichtigen, wie die Eigenschaften der nicht-gaußschen Amplitudenverteilung. Diese Eigenschaften sind im Gegensatz zu der eindeutig beschriebenen rauschförmigen Anregung mit Normalverteilung (siehe z.B. DIN EN 60068-2-64) vielfältiger.

Für die Definition der Eigenschaften von Prüfungen mit klassischer rauschförmiger Anregung werden zwei Indizes verwendet:
• die spektrale Leistungsdichte (PSD) in (m/s²)²/Hz oder g²/Hz und
• der Effektivwert

Für die Prüfung mit nicht-gaußscher Verteilung werden zwei weitere Parameter erforderlich. Diese beiden Werte werden als ganze Zahlen angegeben:
• Kurtosis („Spitzigkeit“)
• Skewness („Schiefe“)

Wahrscheinlichkeitsdichtefunktion

Die Amplitudenwahrscheinlichkeitsdichte-Funktion zeigt die Verteilung der rauschförmigen (oder „zufälligen“) Schwingungen und ermöglicht damit eine Bewertung der Eigenschaften des Signals. In der nachfolgenden Grafik ist der über der Zeit aufgetragene Signalverlauf um 90 Grad gedreht und die Amplitudenwerte sind auf der horizontalen Achse aufgetragen. Anschließend wird die horizontale Achse in feste Intervalle (Bins) unterteilt. Im Histogramm wird nun die Anzahl der Punkte für jedes Intervall gezeigt. Die Histogramme können nicht miteinander verglichen werden, da die Anzahl der Punkte von der Länge des Zeitsignals abhängt, d.h. die Anzahl der Werte steigt mit einem längeren Zeitsignal. Für die Amplituden-wahrscheinlichkeitsdichte-Funktion wird das Histogramm entsprechend der Gesamtanzahl der Punkte des Zeitsignals normalisiert. So erleichtert die Amplitudenwahrscheinlichkeitsdichte den Vergleich von Histogrammen.

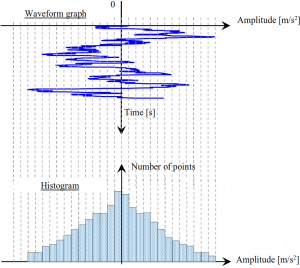
Kurtosis, Maß für die Amplitudenwahrscheinlichkeitsdichte

Der Parameter Kurtosis („Spitzigkeit“) ist ein Maß für die Amplitudenwahrscheinlichkeitsdichte im Bereich von Null (d.h. hier des Mittelwertes). Kurtosis der gaußschen Verteilung ist „3“. Bei einem größeren Wert für Kurtosis wird die Wahrscheinlichkeitsdichte im Bereich von Null und gleichzeitig an den Rändern größer. Nachfolgend ein Beispiel für die Amplitudenwahrscheinlichkeitsdichte bei verschiedenen Werten für Kurtosis.

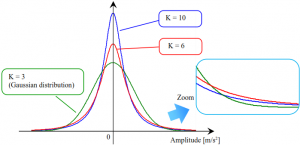
Beispiele für den zeitlichen Verlauf der Signale bei gaußscher Verteilung und Kurtosis = 6 und = 10 sind im folgenden Bild dargestellt. Mit größerem Wert für Kurtosis steigt auch der Spitzenwert der Signale

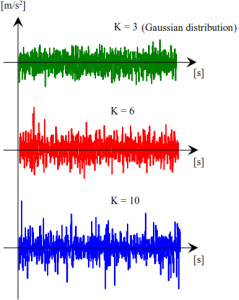
Skewness, ein Maß für die Symmetrie

Skewness („Schiefe“) ist ein Maß für die Symmetrie der Amplitudenwahrscheinlichkeitsdichte. Bei einer Schiefe von „0“ ist die Verteilung symmetrisch zum Mittelwert. Bei von Null abweichenden Werten ist die Amplitudenwahrscheinlichkeitsdichte entsprechend geneigt.

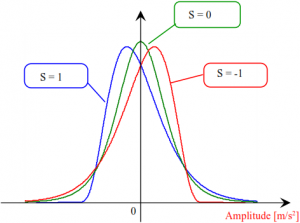
Beispiele für den zeitlichen Verlauf der Signale bei unterschiedlicher Schiefe sind im folgenden Bild dargestellt:

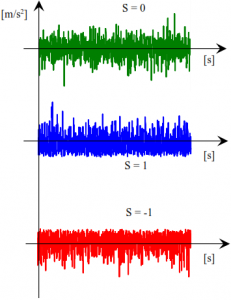
Regelung für nicht-gaußsche Signale

Bei der Regelung für nicht-gaußsche Signale wird, wie auch bei klassischem Rauschen, die spektrale Leistungsdichte (PSD) und der Effektivwert geregelt, so dass diese Werte des Regelkanals mit den Referenzwerten übereinstimmen. Die Werte für Kurtosis und Skewness werden zusätzlich geregelt. So sind bei einem rauschförmigen Versuch mit nicht-gaußscher Anregung der Effektivwert und die Leistungsdichte gleich den Werten für Versuche mit gaußscher Verteilung. Jedoch sind die Spitzenwerte im zeitlichen Verlauf des Signals höher.

Um die nicht-gaußschen Signale genau abbilden zu können, wurde die Regelung des zeitlichen Signalverlaufs eingeführt. Vor der Versuchsdurchführung ist es erforderlich, die Übertragungsfunktion des Systems zu bestimmen:

1. Messen der Übertragungsfunktion
2. Einregeln
Bei diesem ersten Einregeln werden Leistungsdichte und Effektivwert mit den Sollwerten abgeglichen.
3. Einregeln für nicht-gaußsche Verteilung
Es werden nun die Werte für „Kurtosis“ und „Skewness“ mit den Sollwerten abgeglichen.
4. Testbeginn

Vereinzelte und ständige Spitzen

Selbst wenn Kurtosis und Skewness angegeben sind, ist der Zeitverlauf des rauschförmigen Signals nicht eindeutig definiert. Eine weitere Unterscheidung ist möglich.
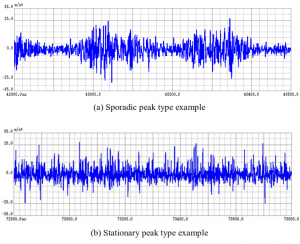
• Vereinzelte Spitzen (Sporadic Peak Type)
Hier treten die Spitzenwerte vereinzelt auf, für diese Art der Anregung kann lediglich ein Wert für Kurtosis angegeben werden.
• Ständige Spitzen (Stationary Peak Type)
Hier treten die Spitzenwerte beständig auf, für diese Art der Anregungen können Werte für Kurtosis und Skweness angegeben werden.

Beispiele für den zeitlichen Verlauf der Signale für die unterschiedliche Charakteristik sind nachfolgend dargestellt.

Schwingprüfsysteme von IMV

Der IMV Schwingungsregler K2 und die IMV Schwingprüfsysteme ermöglichen die Prüfung mit nicht-gaußscher Normalverteilung. Mittels dieses neuen Verfahrens lassen sich die realen Einsatzbedingungen noch besser abbilden und die Prüfungen erzielen genauere Ergebnisse. Dabei können die oben beschriebenen Werte und Charakteristiken verwendet werden.

Darüber hinaus ist es möglich, gemessene Beschleunigungs-Zeitdaten zu analysieren und so die Parameter zur Signalbeschreibung zu ermitteln. Damit kann der Anwender z.B. den RMS-Wert von Signalen zur Zeitraffung erhöhen.

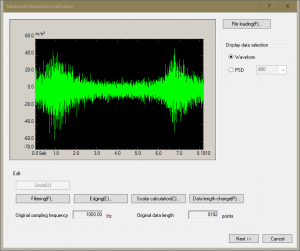
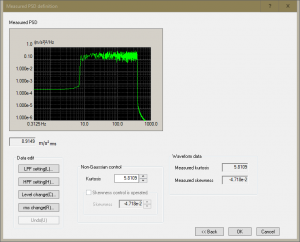
Bei Interesse wenden Sie sich bitte an Martin Engelke, IMV Markteting und Sales Manager, Mobil 0172 1705519.