振動試験とは？試験の種類や仕組みをわかりやすく解説 - なるほど！振動試験

振動試験とは

振動試験とは製品の性能や品質に対し、誰もが共通基盤の上で考え、客観的な認識ができるような科学的に正しいやり方で結論を出すことを可能にする方法が求められており、機械的な振動に関してその試験方法を与えるものが「振動試験」と呼ばれる試験法です。

我々の身の回りには、振動に関係する問題が満ち溢れています。

例えば….

自動車が走るとき、エンジンで発生する振動は車体の各部に伝わる。もしその振動があまりにも激しければ、エンジン付近に取り付けてある部品が故障を起こすかもしれない。起こさないかもしれない。どうやったら、それを見極められるか？
仮にいますぐ故障しなくとも、エンジン振動を受けることでその部品の寿命は短くなっているのではないか？どうやったら、その部品を使用しても大丈夫であることを保証できるか？
走っている道がでこぼこ道なら、車体が激しく揺れる。そのために、車体の各部にやはり振動が発生する。そのために、今聴いていたCD からの音楽が音跳びを起こしてしまった。起こさないようにするため、CD プレーヤーを改造してみたが、改造の効果をどのようにして確かめればよいか？

これらを具体的に実現するための装置が「振動試験装置」です。

振動試験機の仕組み

ここでは振動試験装置の仕組みをご紹介します。

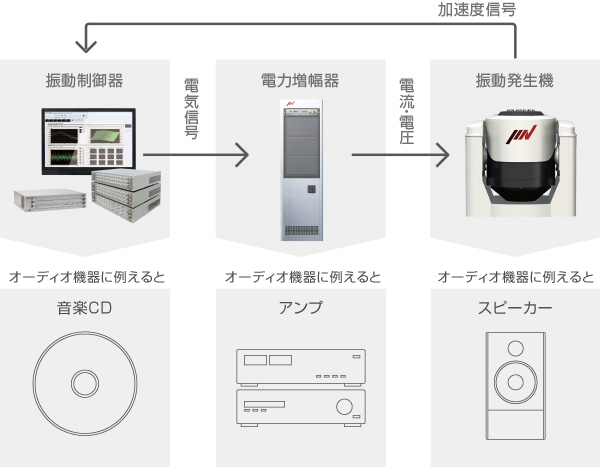
動電式振動試験機

オーディオ機器をイメージしてください。音源のCD等の電気信号をアンプで増幅しスピーカーで空気を振動させ音として伝えます。
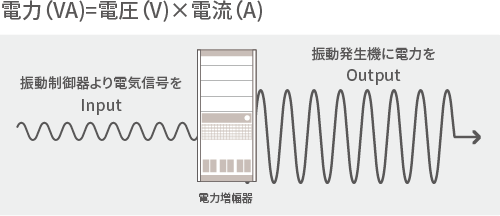
実は動電式振動試験機の振動試験機はスピーカーと同じ原理で動いています。音源の替わりに振動制御器があり、試験条件を登録・実行すると、電力増幅器（アンプ）に電気信号を送り、振動発生機（加振機）を振動させます。
ただ振動制御器はCDデッキなどと大きく違う点があり、振動試験機に取り付けた振動ピックアップの信号をフィードバックさせ、常に振動の状態を把握し試験条件に合うように制御を行っています。

振動発生機（加振機）

振動発生機（加振機）の原理は「フレミングの左手の法則」を用います。磁界中を横切る導線に電流を流すと、直進方向に力が発生し、この力（加振力）により振動テーブルが振動する仕組みです。その力の計算には、下の計算式が用いられます。

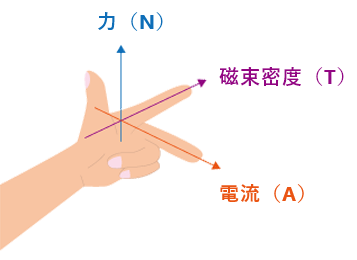
「フレミングの左手の法則」

F：力（N）
B：磁束密度（T）
I：電流（A）
L：電線の長さ（ｍ）

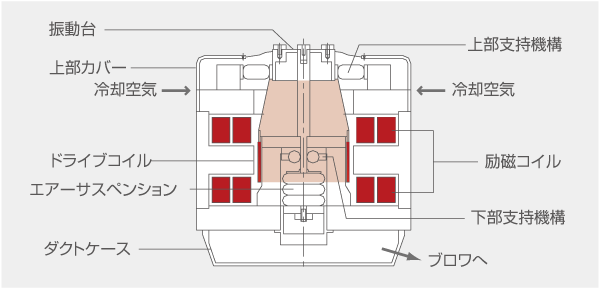
振動発生機（加振機）内部イメージ図（空冷方式）

振動発生機（加振機）
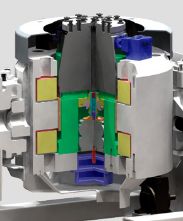
振動発生機（加振機）　断面図

振動制御器

実測した振動データをそのまま電力増幅器に接続し加振しても、残念ながら同じ波形の振動は発生できません。電力増幅器・振動発生機（加振機）の特性により場合によれば全く異なる波形となってしまいます。
振動制御器はこれらの特性を反映させ、自動で目標の振動を発生させるための装置です。IMVの振動制御器「K2」は完全オリジナルの自社開発製品であり、常にお客様の声を大切に使いやすさと性能を向上させるよう努力をしております。最新の「K2」では様々な試験方法をハードウェアを替えずに実行できるだけでなく、PCを使った完全日本語表示のソフトウェアで操作を行うため、複雑な試験も簡単に設定・実行が可能になりました。

振動制御器 K2

K2製品情報ページはこちら
K2画面（一例）

複雑な試験も簡単に設定・実行が可能です。

電力増幅器

電力増幅器の目的は、振動発生機（加振機）に電力を供給することです。
振動制御器からの小さな信号を元に、遥かに大きな電圧・電流を作り上げます。IMVの電力増幅器はスイッチング方式を用い、業界トップレベルの小型・高効率を実現したモジュールを主流とし、省スペース化・省エネに貢献します。

パワーモジュール SA-300
イメージ図

振動試験の種類（正弦波・ランダム波・衝撃波試験）

ここでは正弦波振動試験・ランダム波振動試験・衝撃波振動試験の説明と使用例を紹介します。

正弦波振動試験

一定の周期を持った振動を与える、または一定の周期を掃引させながら振動を与えることが出来る。
固有振動数をもった構造物の近くだと、この試験が必要（例えばファンやモーター）
また、掃引試験をすることでサンプルの固有振動数（＝その製品の弱点）を把握することが出来る。

掃引試験

ある周波数からある周波数まで徐々に振動数を変化させながら、その振動数成分を持った正弦波を順番に連続的に発生させること。波形が連続、かつ時間経過と共に変化する
スポット試験

ある特定の周波数の振動数成分を持った正弦波を一定期間連続して発生させること。同様の波形が続く（同一周波数の場合）

正弦波試験を詳しく見る

ランダム波振動試験

どの瞬間においても、振幅、周波数を予測することが出来ず、統計的な観点でしか記述できない不規則な波形のことである。
ランダム振動を加えると同時に多くの振動数成分で振動させることができるため、共振現象の特性試験などの、振動試験が短時間で実施できる。
車が走っている時の路面からの振動や、ロケットが大気圏を突破し宇宙空間に飛び立つときの振動がこれにあたる。
※現実に起こる振動はほとんどランダム振動と言えます。

ランダム波振動試験を詳しく見る

衝撃波振動試験

その名の通、机をバンと叩いたり車がボンとぶつかった時の振動を再現する。
IMV の制御器では、横軸：時間軸の実測波形を再現する振動を与える際にも使う。

衝撃波振動試験を詳しく見る

その他のIMV受託試験

IMVでは正弦波振動試験、ランダム波振動試験、衝撃波振動試験以外にも幅広く受託試験を取り扱っています。

テストラボトップページはこちら

振動試験加速度とは

振動試験を行う際には、一般的には振動、加速度の設定をして試験を行います。しかし、加速度ってどうやって考えればいいのという質問をよく頂きます。
そのため、今回は振動試験における加速度の考え方についてご紹介していきます。

このコンテンツをよんで頂ければ、今から行って頂く試験の加速度をどのように計算して設定すればいいのかわかるはずです。

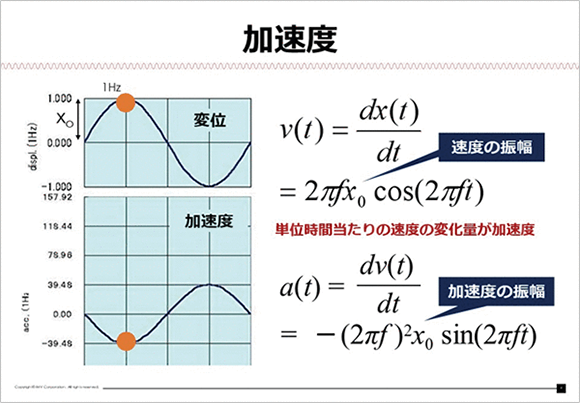
そもそも加速度とは何なのかというところからおさらいしていきましょう！

単位

m/s²

加速度とは

単位時間当たりの速度の変化量を表す量です。つまり速度を時間で微分すると加速度になります。1m/s² であれば、1 秒間にm/s 変化したことを表します。
左上の図の下のグラフが1Hz で振動している物の加速度グラフです。

加速度の計算式

右下の式a(t)=(dv(t))/dt=-(2πf)^2 x_0 sin(2πft) は速度の一般式を時間で微分した式です。cos を微分したのでマイナスのsin に変わっています。速度とはピークの位置がさらに90 度ずれるので変位グラフと一致しますが、マイナスsin なので符号が反転していることがグラフを見ると確認できます。
つまり変位、速度、加速度には時間で微分、積分をすることでそれぞれの値を計算で求めることができるのと、三角関数の比例式になっているので、周期関数の特徴をそのまま利用する事ができ演算処理を行う上で非常に扱いやすい形になっています。